Comparison of an animated character represented first as
a tri-mesh (red) and then as a RLE sparse level set (blue)  [9 MB Quicktime]

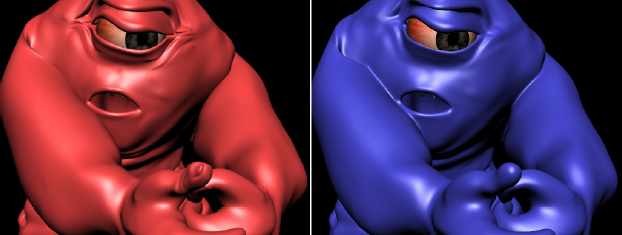
The RLE (run-length encoded) sparse level set is a novel scalable level set representation.  This compact level set representation, and it's ability to represent animated characters, was used in the creation of the "Tar Monster" CG character featured in the movie Scooby Doo 2.

(Please note: this web write-up contains more accurate O-notations than given in the sketch below.)

A. The RLE Sparse Level Set Structure

The novel RLE sparse level set representation has many beneficial characteristics:

(1) highly scalable: +100 million voxel volumes can be presented in less than 15 MB,
(2) fast to access randomly: O( log r ), where r is the number of runs in a single line cross section,
(3) sequential narrow band traversal is near optimal: O( (n²)/D + 1 ) / narrow band element
(4) approximate distance values are provided throughout the bounding volume, and
(5) easily adapted to work with all existing level set methods developed for regular grid structures.

 These advantages are not all shared by the octree [Strain 1999; Frisken 2000], the sparse field method [Whitaker 1998], or the sparse block grid [Bridson 2003] scalable level set representations.

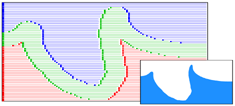
Random Access.  Indexing into individual level set rows is performed using a simple table lookup based on the 2 coordinates perpendicular to the axis of compression. Locating the correct run within a row is done using a binary search after which finding an individual level set value of the run requires just an offset.  Random access thus results O( log r ) time where r is the number of runs in a single row.

Memory Usage. Assuming that in any O(n³) grid there are only O(n²) cells close to the surface, as is the case for smooth enough geometry, the RLE sparse level set structure scales with near optimal, O(n²+R+D), space and time costs, where R is the number of runes, D is the number of defined values and n is the side-length of the bounding volume.

Encoding. Constructing an RLE sparse field structure has both space and time complexity of O(n²+R+D), where n is the side-length of the bounding volume, R is the number of runs and D is the total number of defined voxels.

CSG Operations. Common level set constructive solid geometry (CSG) operations such as union, intersection and subtraction can be performed very efficiently, using only O(n²+R₁+D₁+R₂+D₂) operations when the encoding axes of the input RLE sparse level sets match.
 

B. Representing Traditionally Modeled and Animated Characters Using RLE Sparse Level Sets

Representing an animated polygon-based CG character via a series of RLE sparse level sets in a robust and efficient manner while maintaining fidelity involves solving multiple challenges:

(1) how to create from a polygon mesh an RLE sparse level set with a bounding volume of n³ voxels in less than O(n³) operations,
(2) robustness in the presence of imperfectly closed meshes, which are quite commonly produced by traditional polygon-character modeling and animation techniques, and
(3) how to avoid temporal anti-aliasing issues that could arise from the inability of regular level sets to represent features smaller than the voxel widths.

C. Summary

The RLE sparse level set structure, or structures based on it's general design, will most likely have significant uses in the field of physical simulation-based computer graphics.  Obvious areas where the RLE sparse level set structure can be applied are (a) fluid simulation [Enright et al. 2002; Houston et al. 2003], (b) rigid-body dynamics [Guendelman et al. 2003], (c) soft-body dynamics [Irving et al. 2003] and (d) cloth simulation [Bridson et al. 2002].

 

Houston, B., Wiebe, M. & C. Batty.  (2004)  "RLE Sparse Level Sets."  Proceedings of the SIGGRAPH 2004 Conference on Sketches & Applications. ACM Press. [PDF]  (Supplemental Materials [PDF])

 

@inproceedings{
   author = {Ben Houston and Mark Wiebe and Christopher Batty},
   title = {RLE Sparse Level Sets},
   booktitle = {Proceedings of the SIGGRAPH 2004 Conference on
       Sketches \& Applications},
   year = {2004},
   location = {Los Angeles, California},
   publisher = {ACM Press},
   }