Explorations in 4-Peg Tower of Hanoi Supplemental Web Materials:         ► 2D and 3D Visualizations of State Transition Graphs         ► A Distributed Solver for Tower of Hanoi Problems

Distributing Memory and Processing Across Machines

It is difficult to reduce the memory requirements of solving the Tower of Hanoi problem without significantly increasing the running time of the solver on a single machine. However, we have come up with a distributed solution for Tower of Hanoi. The idea is to arrange n-computers into a ring, where:

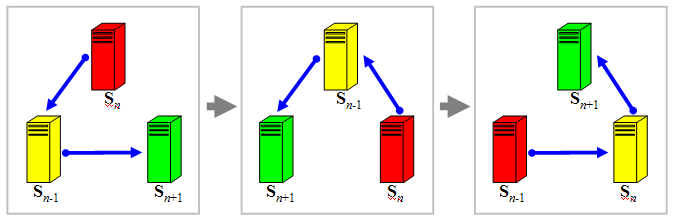
This distributed solution is theoretically scalable to any number of computers - allowing one to postpone the point at which memory problems overwhelm the solver.

We estimate that, given a dozen computers with at least 1 GB of RAM each, one could figure out up to ToH(4,22) in a week or so of processing time. As a proof of concept, we implemented a prototype distributed solver, which can run on 3 machines at once. (For decent speed it requires at least 100Mbit Ethernet, and preferably gigabit Ethernet.)

Algorithm for Three Machines

Given three machines, we assign each one a distinct role: an S_n-1 client, an S_n client and an S_n+1 client.

The operation of the cluster is as follows:

Startup The S_n client will be initially seeded with the starting state. Both the S_n-1 and the S_n+1 clients will have their stores empty.

Step 1 The S_n client generates all the adjacent states to the states in its store and sends those new states to the S_n-1 client. The S_n-1 client compares all the states it receives from the S_n client against its store and only sends the ones that are not present in its store to the S_n+1 client. The S_n+1 client adds the states it receives from the S_n-1 client to its store if the states are not already present.

Step 2 After the S_n client has send all adjacent states to the S_n-1 client, the S_n-1 client has sent its last state to the S_n+1 client and the S_n+1 client has processed the final state from S_n-1, the clients will rename themselves using the following mapping: S_n+1 → S_n, S_n → S_n-1, S_n-1 → S_n+1.
Now go to step 1 if a halting state has not yet been found.

Figure 1: The inter-machine Tower of Hanoi state flow across three complete iterations of the three machine algorithm.
 

For more information please see:

Ben Houston and Hassan Masum.  "Explorations in 4-peg Tower of Hanoi."  Carleton University Technical Report TR-04-10, November 2004.